Publications

AutoFT: Robust Fine-tuning By Optimizing Hyperparameters on OOD Data

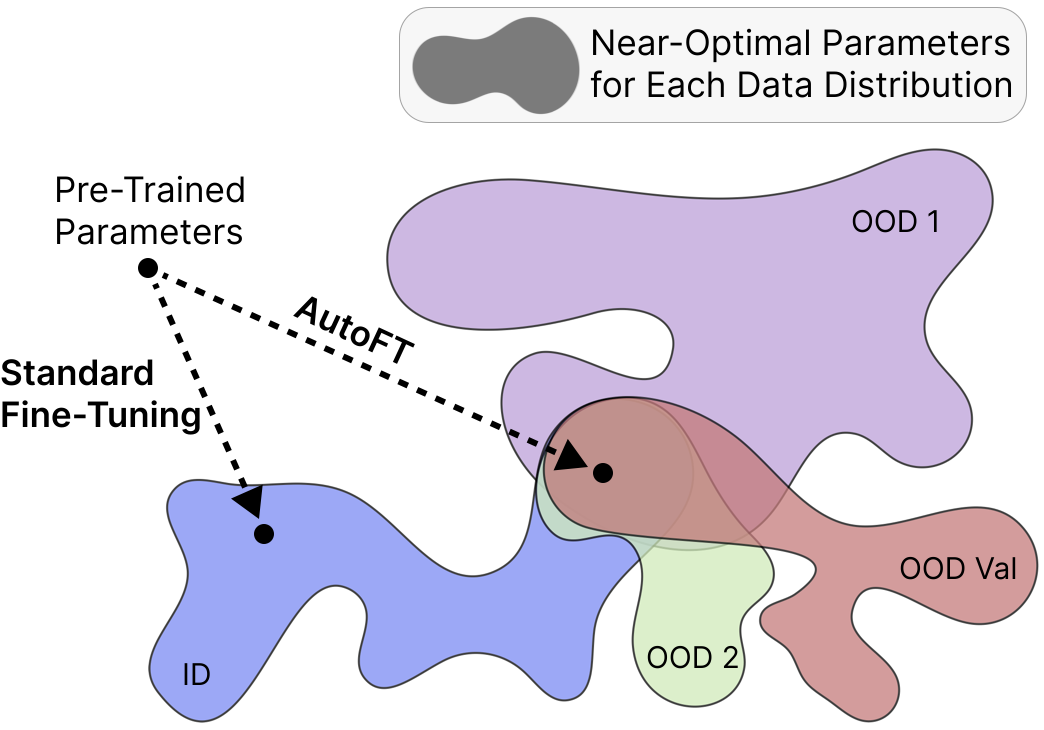
Caroline Choi*, Yoonho Lee*, Annie Chen, Allan Zhou, Aditi Raghunathan, Chelsea Finn

Preprint

AutoFT is a data-driven approach to robust fine-tuning for foundation models. AutoFT searches for a robust fine-tuning procedure for a given task by optimizing hyperparameters on a small OOD validation dataset. AutoFT attains new state-of-the-art performance on the ImageNet, WILDS-iWildCam, and WILDS-FMoW distribution shift benchmarks.

Selected Papers Adaptation, Robustness,

Symbol Length in Brauer Groups of Elliptic Curves

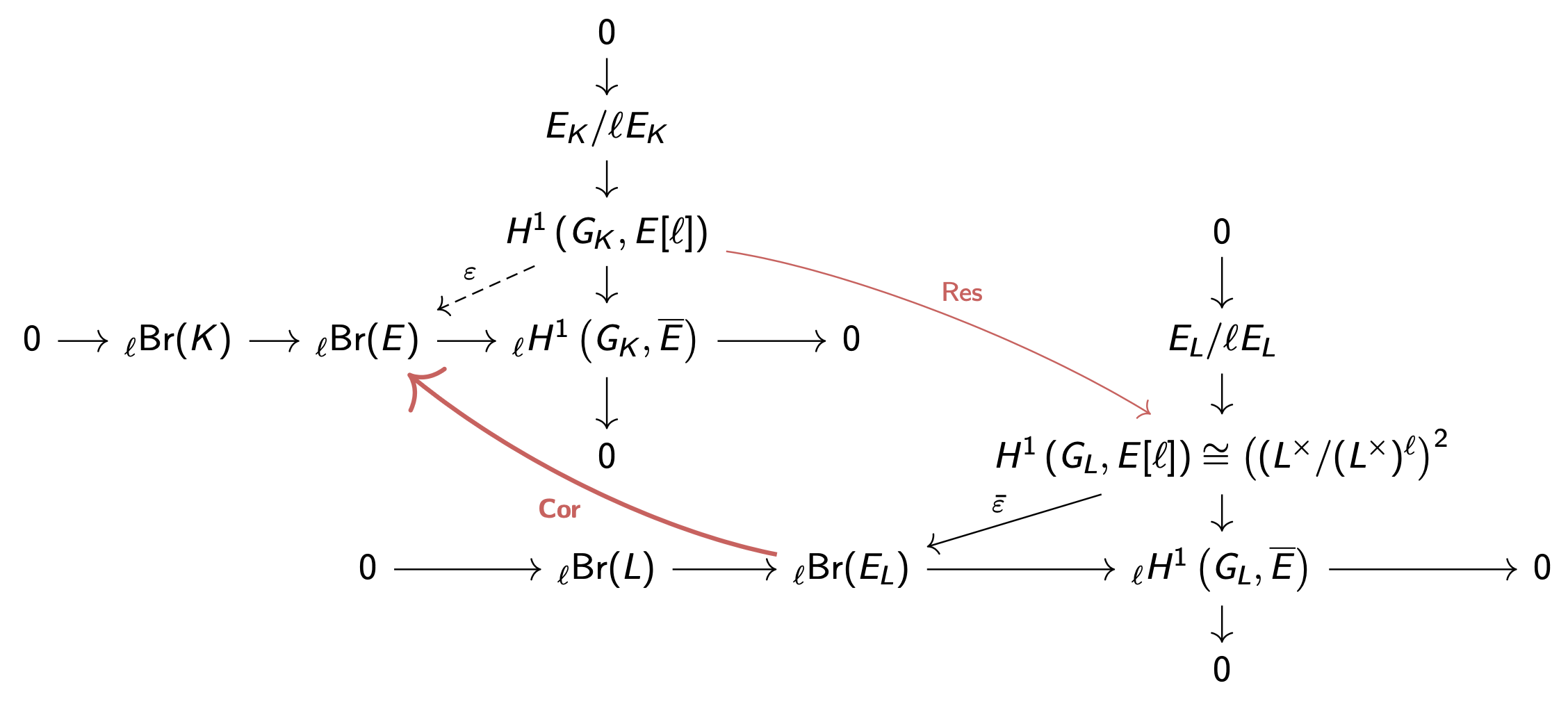
Mateo Attanasio*, Caroline Choi*, Andrei Mandelshtam*, Charlotte Ure*

Proceedings of the American Mathematical Society

The Brauer group is a tool that helps us understand the shape and characteristics of a mathematical space, known as a variety. We study Brauer groups of elliptic curves and improve bounds on a measure of their complexity, known as symbol length.

Mathematics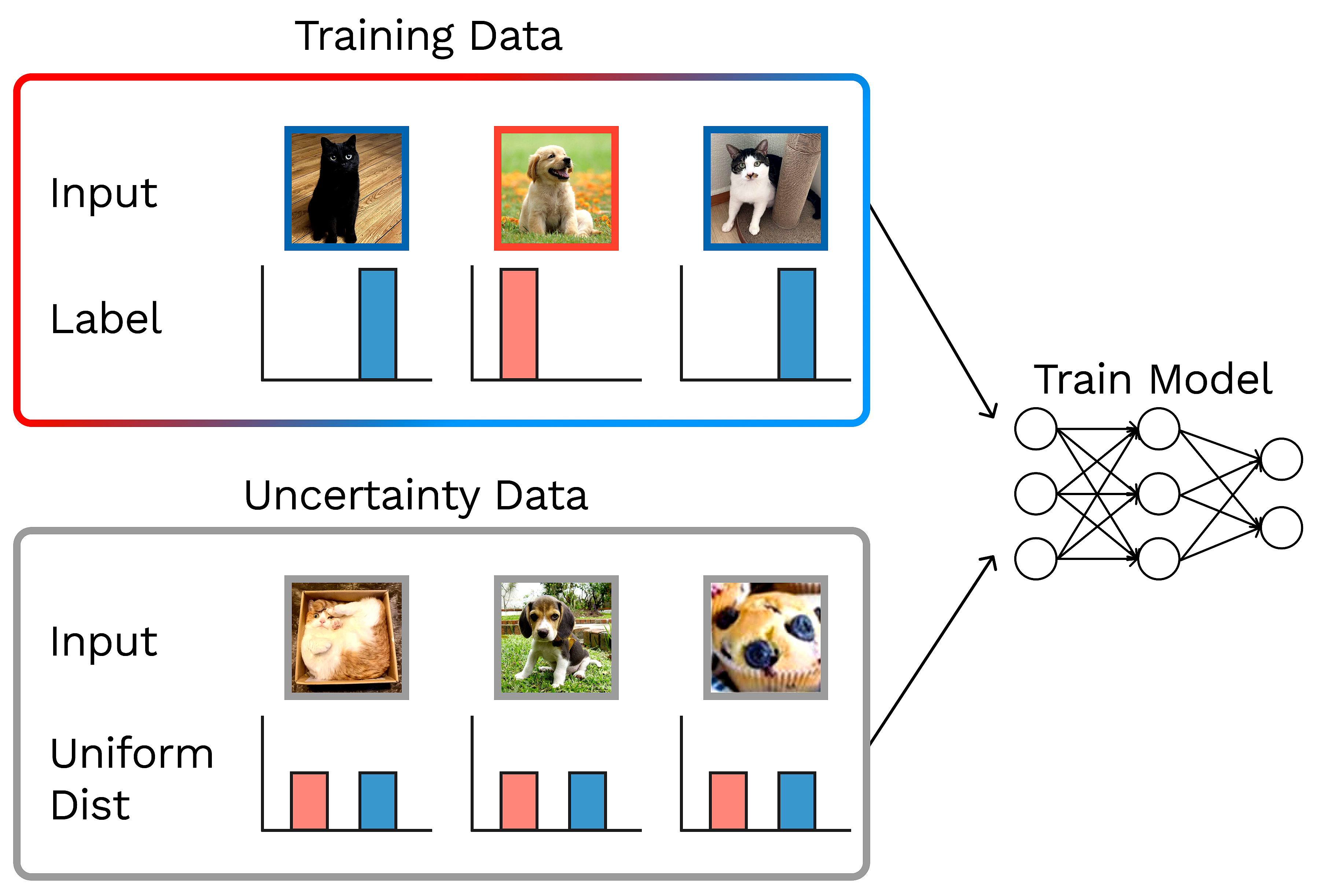

Conservative Prediction via Data-Driven Confidence Minimization

Caroline Choi*, Fahim Tajwar*, Yoonho Lee*, Huaxiu Yao, Ananya Kumar, Chelsea Finn

ICLR 2023 Workshops: TrustML, ME-FOMO

Data-Driven Confidence Minimization (DCM) is a framework for training models to make conservative predictions in safety-critical settings. We find that confidence minimization on a good choice of uncertainty dataset provably detects out-of-distribution examples and also yields improvements for selective classification.

Selected Papers Robustness, Safety,

Wild-Time: A Benchmark of In-the-Wild Distribution Shift Over Time

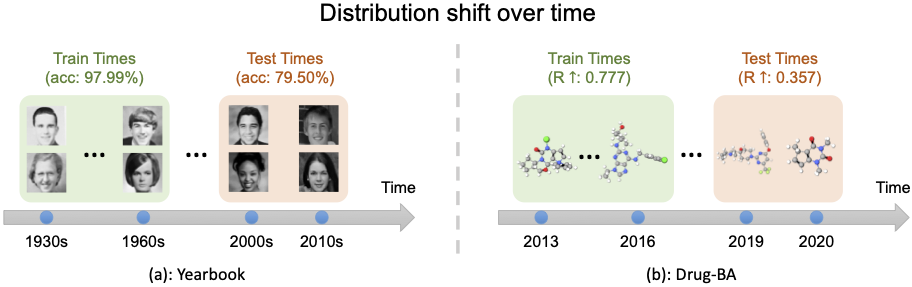
Huaxiu Yao*, Caroline Choi*, Bochuan Cao, Yoonho Lee, Pang Wei Koh, Chelsea Finn

NeurIPS 2022

Wild-Time is a benchmark for real-world distribution shifts over time. We curated five datasets that exhibit temporal shift and span diverse applications and data modalities. We benchmark methods from the continual learning and domain generalization literature and find that no approach consistently outperforms ERM.

Selected Papers Benchmarks, Robustness,

On Class Numbers, Torsion Subgroups, and Quadratic Twists of Elliptic Curves

Talia Blum*, Caroline Choi*, Alexandra Hoey*, Jonas Iskander*, Kaya Lakein*, Thomas Martinez*

Transactions of the American Mathematical Society

We prove new bounds on the class number, first conjectured to exist by Gauss in 1801. We leverage connections between number theory and algebraic geometry, and construct a new family of maps between ideal class groups and elliptic curves.

Mathematics

On Permutation Weights and q-Eulerian Polynomials

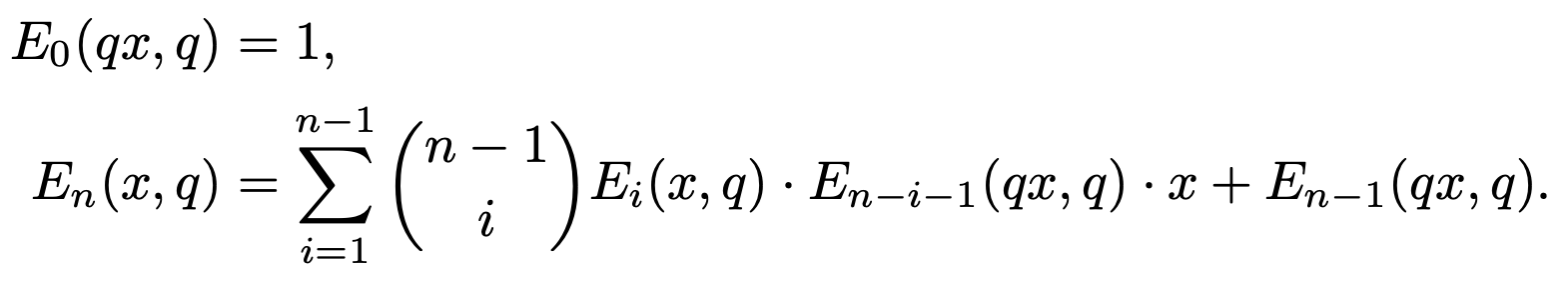
Aman Agrawal*, Caroline Choi*, Nathan Sun*

Annals of Combinatorics

We proved a "stabilization" conjecture by Gunnells et al. (2019) arising in the study of new permutation statistics known as weights. We prove this conjecture, and further show that permutation weights exhibit a recurrence relation.

Mathematics